【無料の学習プリント】小学4年生の算数ドリル_展開図の考え方
今回のプリントは、「小学4年生の算数ドリル_展開図の考え方」です。
前回まで「立方体と直方体」のプリントを制作しましたが、うちの子はどうも展開図が苦手らしく、なかかな頭に入っていかないようでした。
そこで、「立体を展開図にしたときに面がどのように移動するか」の補足のプリントを作りました。もし、展開図が苦手のようだというお子さんは参考にしてみてください。
※解答PDFで間違っている箇所がありましたので修正しました。(2021.06.14)
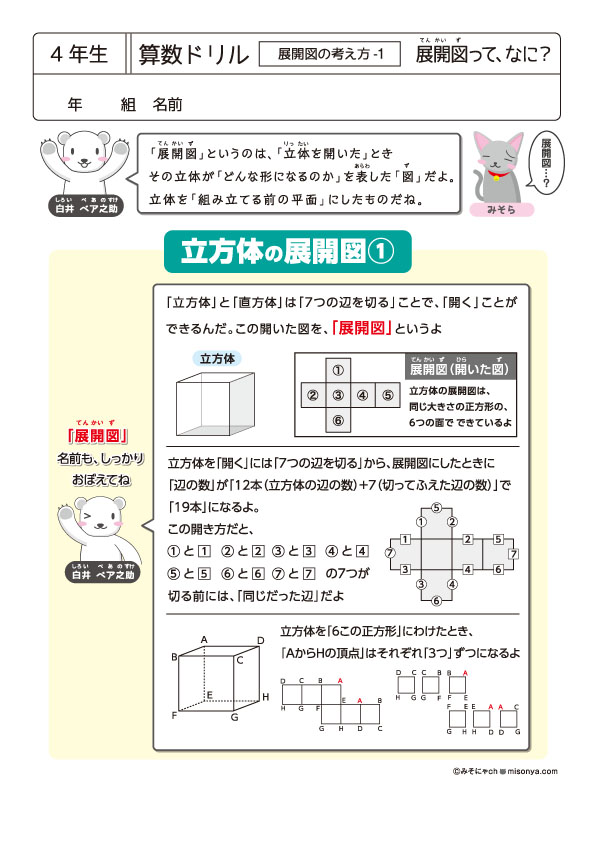
サンプル問題です。問題PDFは全4ページ分。
下記よりDLしてください。
「展開図」にしても「2つの面が共有している辺は変わらない」
立方体や直方体を「展開図」にしたとき、「元の面が、どこにどのような方向で対応しているか」というのは、これまでの算数学習でうちの子が一番手間取ったところです。
なので私がうちの子に、「立体を展開図にしたときに面がどのように移動するか」を説明したものをプリントにしました。
もっとわかりやすい方法もあるんでしょうけど、少なくともうちの子は「私の説明」で理解できたみたいです。
まぁ、大切なのは1か所で、「くっついている2つの面が、どの辺を共有しているか」です。
「共有している1つの辺」がわかると、その辺が「それぞれの面のどの位置(上下左右)の辺に当たるのか」を確認することで、「展開したことで面がどのような方向に向いたのか」がわかります。
具体的には、「面ABCD」と「面CDEF」が「辺CD」を共有してくっついているとき、「面ABCD」の「右の辺」が「辺CD」で「面CDEF」の「上の辺」が「辺CD」なら、「面ABCD」の「右側」に「面CDEF」が「上向き」にくっついていることになります。
立方体や直方体を「どのように展開」しても、くっついている辺は変わりません。
だって、立体のときからくっついたままなんですから。
「展開図」にしても「2つの面が共有している辺は変わらない」。
この「変わっていない辺」を目印にして、「展開したときに面の位置がどのように変化したのか」をしることができる。
このことが「わかっているかどうか」で、展開図の問題の難易度が変わると思いますので、お子さんがうちの子のようにわかっていないようでしたら、教えてあげてください。
では、また。
